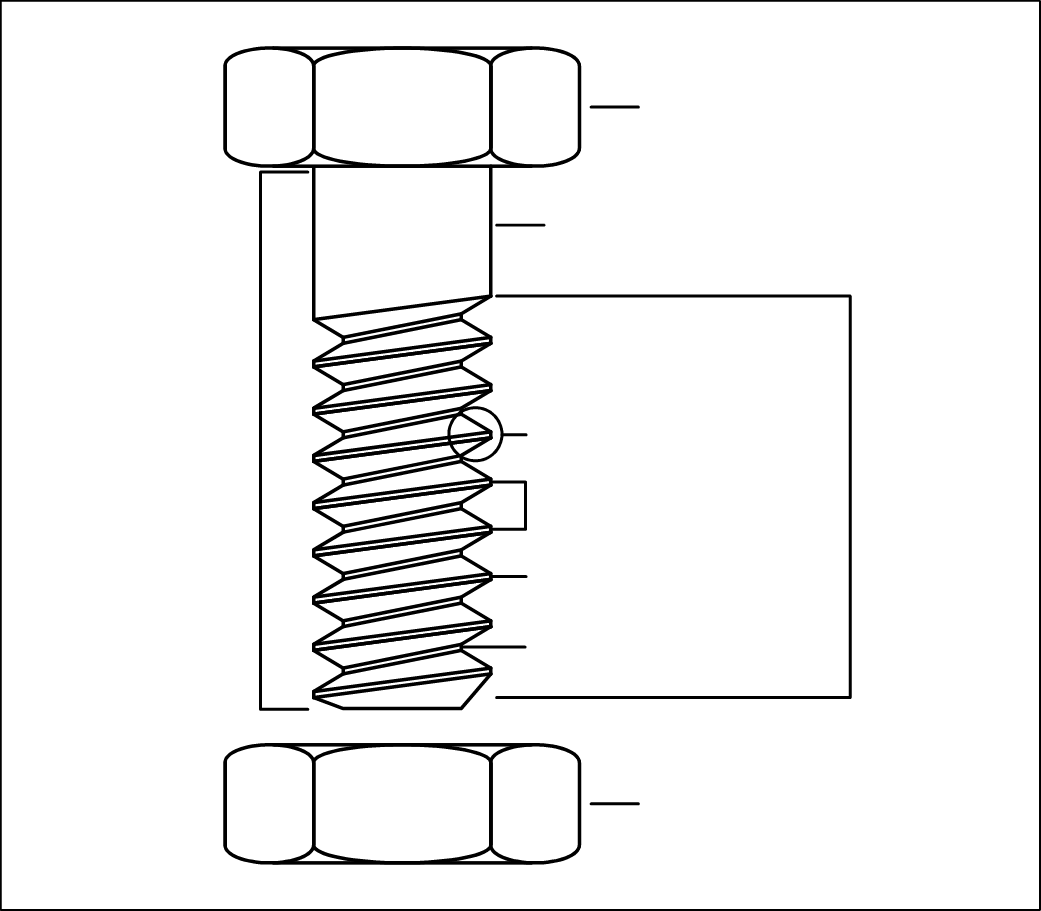
Tornillos¶
Un tornillo es una máquina simple formada por un plano inclinado que se encuentra enrollado alrededor de un eje cilíndrico.
Índice de contenidos:
Partes de un tornillo¶
Las diferentes partes del tornillo reciben los siguientes nombres.
- Vástago
- Parte cilíndrica del tornillo donde se tallan los surcos de la rosca.
- Cuello
- Parte del vástago del tornillo que no está roscada.
- Rosca
- Plano inclinado enrollado de forma helicoidal alrededor del vástago.
- Cabeza del tornillo
- Parte extrema del tornillo que se utiliza para hacerlo girar. En tornillos grandes suele ser de forma cuadrada o hexagonal.
- Filete
- Parte saliente del surco de la rosca.
- Paso
- Distancia que hay entre dos crestas consecutivas de la rosca.
- Tuerca
- Pieza mecánica con un orificio roscado que se acopla al tornillo. Suele tener forma cuadrada o hexagonal para facilitar su giro mediante llaves de apriete.
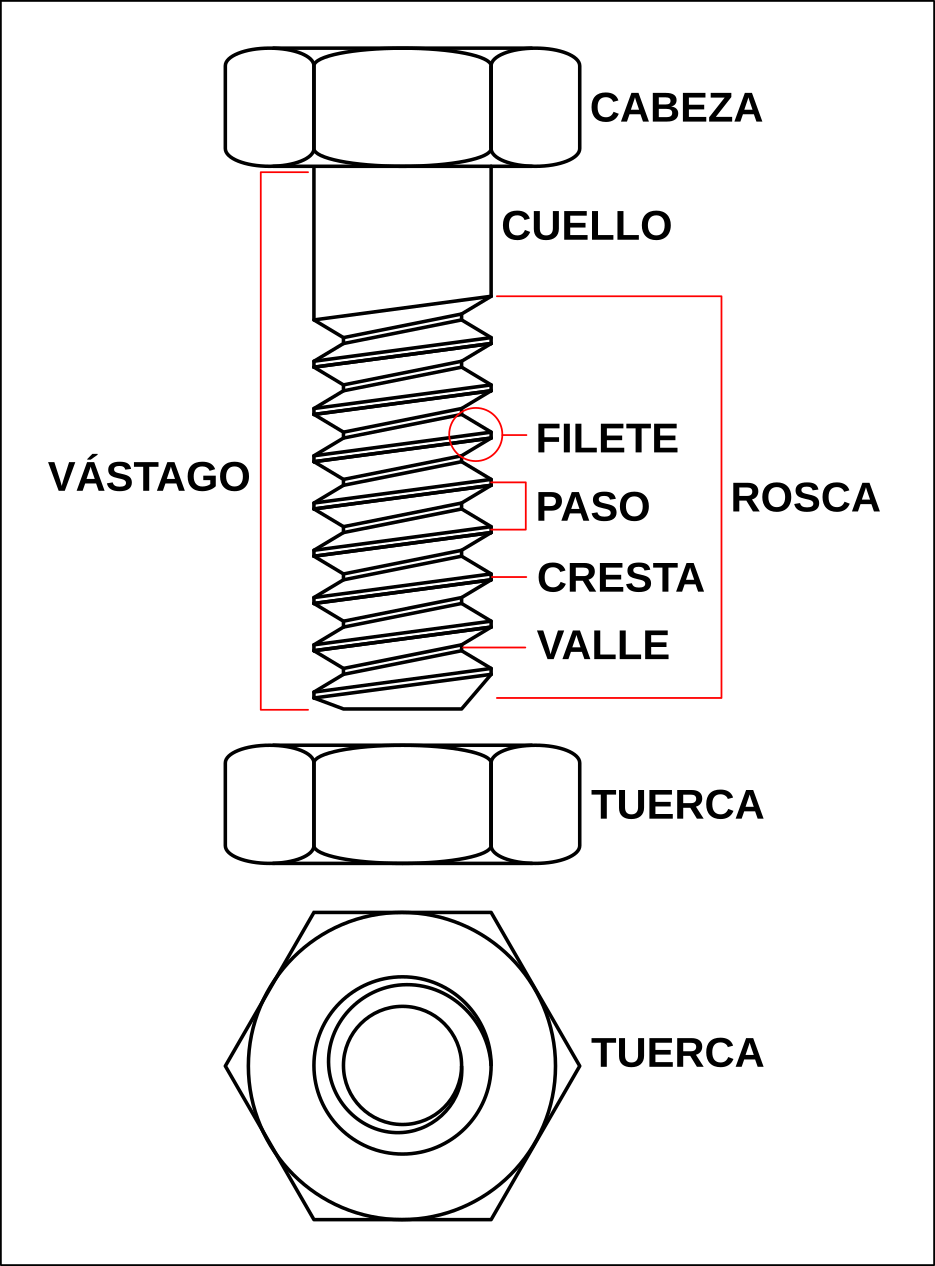
Partes de un tornillo y tuerca hexagonal.¶
Aplicaciones de los tornillos¶
- Uniones desmontables
Una de las aplicaciones de los tornillos es realizar uniones desmontables, es decir, uniones que se pueden montar y desmontar con facilidad.
Por ejemplo, la carcasa de un ordenador está unida con tornillos.
- Mecanismos que avanzan con precisión
Los tornillos permiten realizar movimientos muy precisos.
Por ejemplo, el tornillo de un grifo giratorio permite abrir o cerrar el paso de agua con mucha precisión. Otro ejemplo son las sillas a tornillo, que se pueden subir o bajar poco a poco dando vueltas al asiento.
- Mecanismos para mover con fuerza
Otra aplicación importante de los tornillos es la construcción de mecanismos que avanzan con mucha fuerza.
Por ejemplo, el mecanismo de un gato mecánico está basado en un tornillo que mueve un sistema de tijeras con suficiente fuerza como para levantar un automóvil.
Cálculo de tornillos¶
Los principales parámetros de un tornillo son su paso, el número de vueltas de giro y el avance lineal que se obtiene al girarlo.
La relación entre estas magnitudes se expresa mediante la siguiente fórmula:
Donde:
Avance = distancia lineal que recorre el tornillo en milímetros.
Giro = número de vueltas que gira el tornillo.
Paso = distancia que avanza el tornillo por cada vuelta que gira.
Tanto el Avance como el Paso deben expresarse en las mismas unidades de longitud, normalmente milímetros.
Ejercicio silla¶
Una silla de taller se eleva mediante un tornillo con una rosca de paso igual a 4 milímetros por vuelta. Si queremos elevar la silla 6 centímetros ¿Cuántas vueltas será necesario dar al tornillo?
Para resolver el problema, escribimos primero los datos disponibles, convirtiendo todas las distancias a la misma unidad.
A continuación escribimos la fórmula y sustituimos las cantidades conocidas:
Para finalizar, despejamos la incógnita para hallar el resultado:
Ejercicio tornillo de banco¶
Un tornillo de banco se abre una distancia de 12 centímetros tras girar la manivela un total de 40 vueltas. ¿Cuál es el paso del tornillo?
Para resolver el problema, escribimos primero los datos de los que disponemos, convirtiendo todas las distancias a la misma unidad.
A continuación escribimos la fórmula y sustituimos las cantidades conocidas.
Para finalizar, despejamos la incógnita para hallar el resultado.
Ejercicio tornillo de microscopio¶
Un microscopio dispone de un tornillo para subir y bajar la platina y poder enfocar correctamente el objeto que se desea observar. Si el paso del tornillo es de 0,5 milímetros y realizamos un giro de 16 vueltas ¿cuánto avanzará la platina?
Para resolver el problema, escribimos primero los datos disponibles, convirtiendo todas las distancias a la misma unidad.
A continuación escribimos la fórmula y sustituimos las cantidades conocidas.
Para finalizar, no hace falta despejar y podemos calcular directamente el resultado.
Ejercicios¶
¿Qué es un tornillo?
Nombra las nueve diferentes partes de la siguiente imagen:
¿Qué es el paso de un tornillo?
¿Qué tres aplicaciones tienen los tornillos? Escribe un ejemplo de cada una de las aplicaciones.
¿Por qué crees que los tornillos permiten producir movimientos de avance con mucha precisión?
Una prensa utiliza un tornillo para cerrar su mordaza. El tornillo tiene un paso de 6 mm por vuelta. Si queremos cerrar la prensa 18 cm, ¿cuántas vueltas debemos dar al tornillo?
Un elevador mecánico sube una plataforma 2 metros mediante un tornillo de paso 10 mm por vuelta. ¿Cuántas vueltas del tornillo son necesarias para subir la plataforma?
El tornillo que ajusta la altura de la aguja de una máquina de coser tiene un paso de 1 mm. Si queremos bajar la aguja 5 mm, ¿cuántas vueltas hay que dar al tornillo?
Un tornillo de una prensa de laboratorio permite abrir 40 mm tras dar 25 vueltas. ¿Cuál es el paso del tornillo?
Un tornillo de una prensa hidráulica sube el pistón 0,75 m mediante 150 vueltas. ¿Cuál es el paso del tornillo?
Una mordaza de banco se desplaza 15 centímetros tras girar la manivela 60 vueltas. ¿Cuál es el paso del tornillo?
Una prensa de carpintero se ajusta mediante un tornillo con paso de 5 mm por vuelta. Si giramos la manivela 12 vueltas, ¿cuánto se desplazará la mordaza?
Una silla de laboratorio tiene un tornillo con paso de 2 mm por vuelta. Si se dan 25 vueltas al tornillo, ¿cuánto se eleva la silla?
Una sierra de banco tiene un tornillo de ajuste del soporte con paso de 1,5 mm por vuelta. Si giramos la manivela 40 vueltas, ¿cuánto se desplazará el soporte?
Unidad imprimible¶
Unidad en formato imprimible, con preguntas.