Gears¶

A gear is a mechanism made up of two or more toothed wheels. It is used to transmit circular movement and to transform speed and turning force.

If the two wheels are of different sizes, the larger wheel is called crown and the smaller wheel is called pinion.

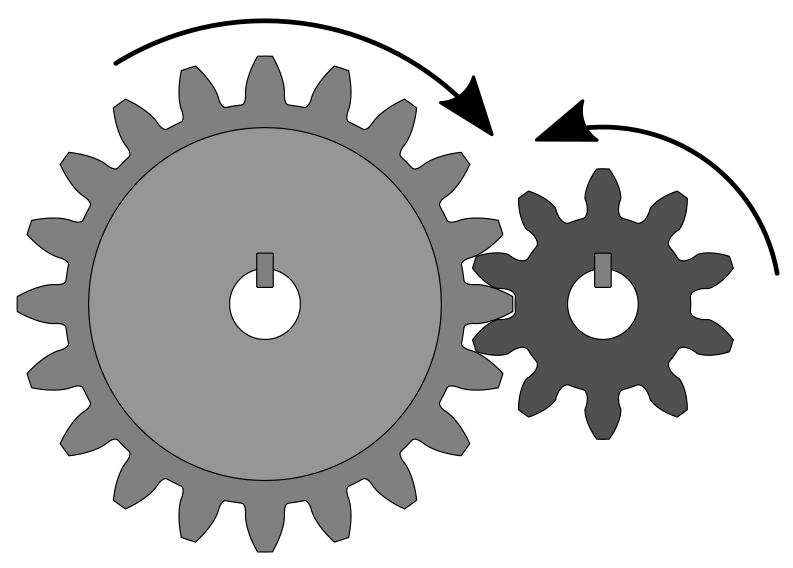
Engranaje de corona y piñón con flechas de sentido de giro

Crown and pinion gear with arrows for direction of rotation.¶

One of the most important applications of gears is the transformation of the speed of rotation from a motor, generally fast and with little torque, to the application that has to do work, generally slower and with more torque.

For example, with gears, the speed of rotation of a car engine is transformed to a lower speed and with greater torque, of the wheels of the car.

Motor torque¶

Motor torque is equivalent to the 'force' with which a shaft turns. The name buoyant force is usually reserved for the case of a force acting in a straight line. In the case of rotating axes, the motor torque indicates what rotating force would have to be applied at a distance of one meter from the axis of rotation to produce the same effect.

For example, a turbo diesel utility car engine usually has an approximate torque of 250 Newton·meter. This motor torque would be equivalent to pushing a rotating shaft with a lever one meter long, applying 250 Newtons at the end (about 25 kilograms-force).

Gears increase motor torque (turning force) in the same proportion as they reduce turning speed. In the case of a gear that increases the rotation speed, the motor torque will be reduced in the same proportion. These proportions occur in all mechanisms that transform movements.

A mechanism that multiplies force will, in turn, reduce the distance or speed of movement.

Gear calculation¶

The speed of rotation of each toothed wheel of a gear depends on the number of teeth.

The formula that relates the speeds of two toothed wheels equals the product of the number of teeth by the angular speed according to the following formula.

$Z_{1} \cdot N_{1} = Z_{2} \cdot N_{2}$

Being

Z1 = Teeth of the first sprocket

N1 = Angular speed of the first gear

Z2 = Teeth of the second sprocket

N1 = Angular speed of the second gear

Angular velocity is usually measured in revolutions per minute also written as rpm, which means the number of complete revolutions the wheel turns in one minute. A typical motor usually has an angular velocity in the range from 1,000 rpm to 6,000 rpm.

Wind turbine exercise¶

In this case we are going to calculate a gear that is used to multiply the speed of rotation of an axis.

A wind turbine rotates its blades at a speed of 20rpm and you must multiply that speed up to the speed of the generator which is 1000rpm. If the pinion connected to the generator has 15 teeth, how many teeth will the crown have?

The first step will be to write the data of the problem.

$N_{1} = 20 \: rpm$

$N_{2} = 1000 \: rpm$

$Z_{2} = 15 \: teeth$

Next we write the formula and substitute the known values.

$Z_{1} \cdot N_{1} = Z_{2} \cdot N_{2}$

$Z_{1} \cdot 20 \: rpm = 15 \cdot 1000 \: rpm$

Finally we solve the equation and calculate the value of the unknown.

$Z_{1} = \cfrac{15 \cdot 1000 \: rpm}{20 \: rpm}$

$Z_{1} = 750 \: teeth$

In practice, when the tooth ratio is so large, gear trains with more than two interconnected wheels are often used to reduce or increase the rotational speed in several stages.

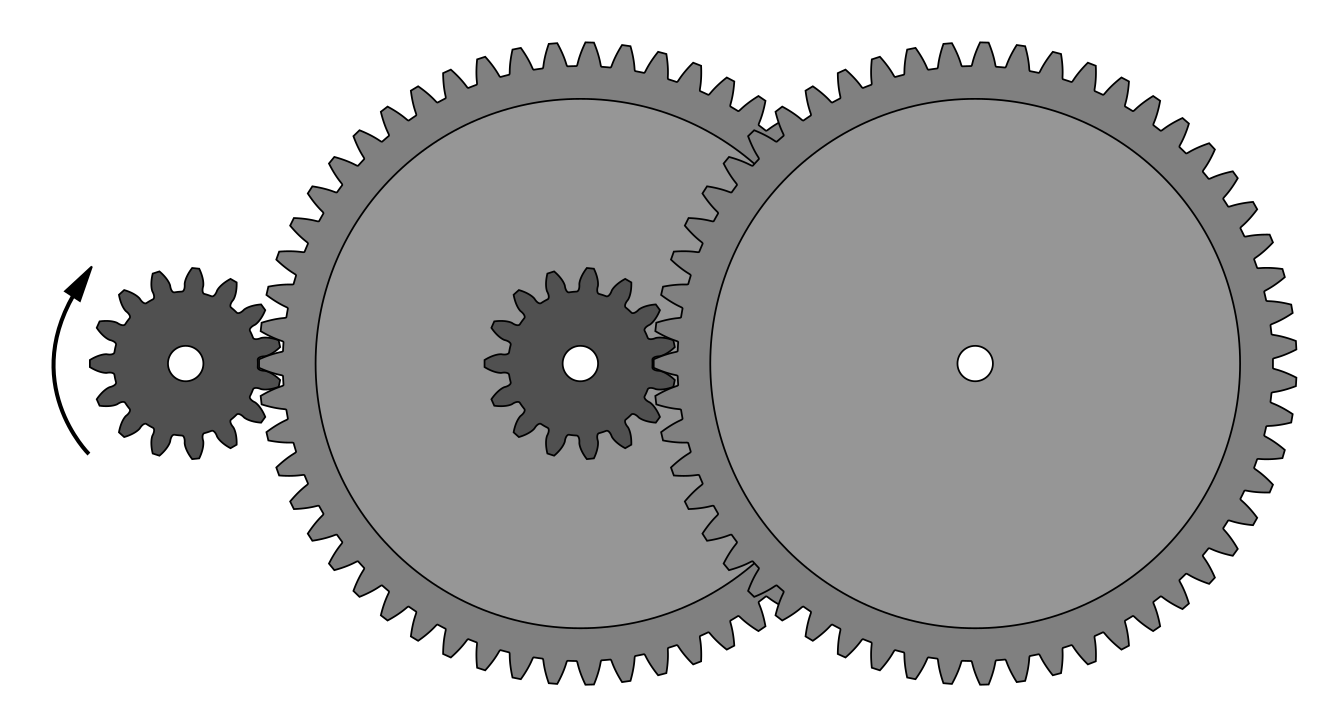
Tren de engranajes que reducen mucho la velocidad de giro del piñón

Gear train that greatly reduces the speed of rotation of the pinion¶

Ejercicio automóvil eléctrico¶

Un automóvil eléctrico tiene el motor conectado mediante un engranaje reductor a las ruedas. Sabemos que la velocidad máxima del motor es de 9000rpm y que la velocidad máxima de las ruedas es de 1500rpm. Si el número de dientes del engranaje más pequeño debe ser de 8 ó más dientes ¿Cuantos dientes debe tener cada engranaje?

Este ejercicio permite varias soluciones válidas porque no especifica el tamaño del piñón.

El primer paso será escribir los datos del problema. El motor estará conectado al primer engranaje y las ruedas al segundo engranaje.

$N_{1} = 9000 \: rpm$

$N_{2} = 1500 \: rpm$

El engranaje 1 conectado al motor es el que gira más rápido y, por lo tanto, es el engranaje más pequeño de los dos. Ahora vamos a escoger un tamaño para este engranaje pequeño, que sea igual o mayor de 8 dientes.

$Z_{1} = 10 \: teeth$