8. La porta lògica xor

La porta de la lògica Xor té dues o més entrades i una sortida.

La sortida té un valor lògic elevat (1) Si la suma de les entrades és un valor estrany.

És a dir, si l’entrada a ** o ** Entrada B està a nivell alt, però no ambdues alhora, la sortida serà a un nivell alt. D’aquí el nom de ** exclusiu o ** en anglès.

El símbol de la porta ** xor ** és el següent:

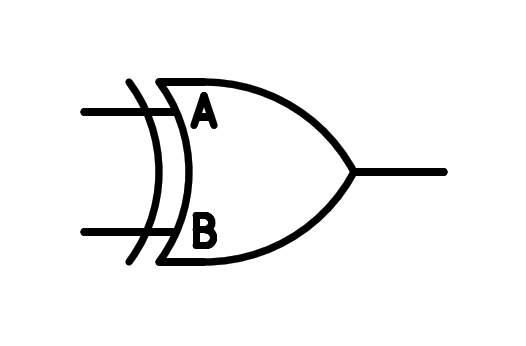
Puerta lógica XOR de dos entradas.

Símbol de la porta lògica de dos entrades.

La funció lògica de la porta Xor ** està representada per un símbol de suma envoltat d’un cercle, de manera que la sortida de la porta serà la lògica exclusiva de les entrades:

Out = a \ oplus b

La ** Taula de veritat xor ** és la següent:

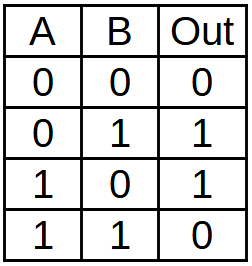
Tabla de verdad de la puerta lógica XOR de dos entradas.

Taula de veritat de la porta lògica xor de dues entrades.

Si les dues entrades valen zero, la sortida valdrà zero, si alguna entrada val una, la sortida valdrà una i si les dues entrades valen una, la sortida es tornarà a valorar.

Aplicacions de portes XOR

  1. La porta XOR es pot utilitzar per calcular el valor de paritat de totes les seves entrades, de manera que les entrades al costat de la sortida sempre tindran un valor uniforme d'alguns.
  2. Una altra aplicació de portes XOR és fer sumes de bits aritmètics. La porta XOR calcula la suma aritmètica de dos bits i la porta i calcula el transport d’afegir dos bits.
  3. Una altra aplicació de portes XOR és invertir o no invertir el valor de l’entrada B depenent de l’entrada a:
    • Si l’entrada a l’exterior zero, l’entrada B es copia igual a la sortida.
    • Si l’entrada a Vale One, l’entrada B es copia ** invertida ** a la sortida.

Simulació

A la simulació següent podem veure el funcionament de la porta lògica XOR.

Exercicis

  1. Expliqueu amb les vostres paraules el funcionament de la porta lògica xor.

  2. Dibuixa el símbol de la porta lògica XOR de dues entrades, la seva funció lògica i la seva taula de veritat.

  3. Expliqueu breument tres aplicacions de la porta lògica xor.

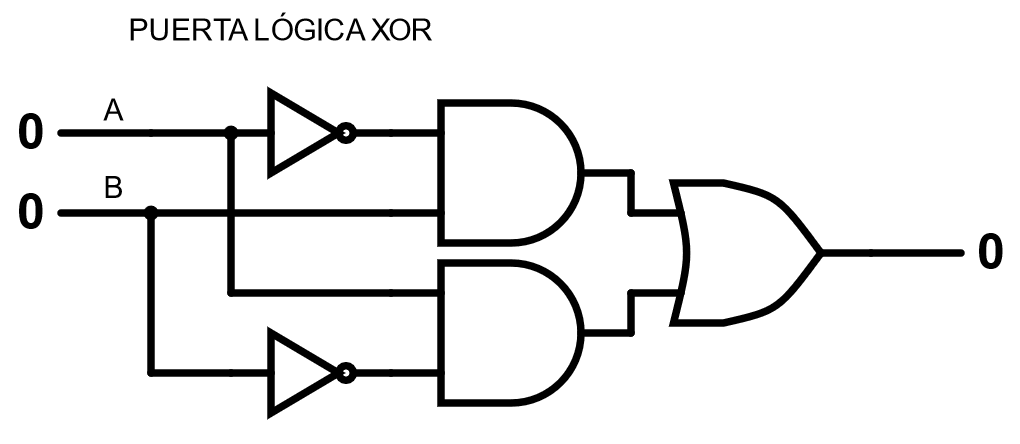
  4. Al simulador, copieu el circuit que apareix a la imatge següent per emular el funcionament de la porta xor a través de no, o i: i:

    Puerta XOR simulada con puertas NOT, OR y AND.

    Comproveu que la seva operació sigui igual a la porta xor.

  5. Dibuixa una porta lògica de tres entrades, la seva funció lògica i la seva taula de veritat.

    Per realitzar la taula de veritat de la porta, recordeu que la sortida val una si els bits d’entrada són estranys.