4. The binary system

Digital electronics operate with two valid values, on and off. The binary system is a numbering system that only uses two figures, zero (0) and one (1), so it is very adaptable well to represent the two states of digital electronics.

Almost all modern computers are based on digital electronics and their numbering and information representation system is the binary system.

Counting in binary

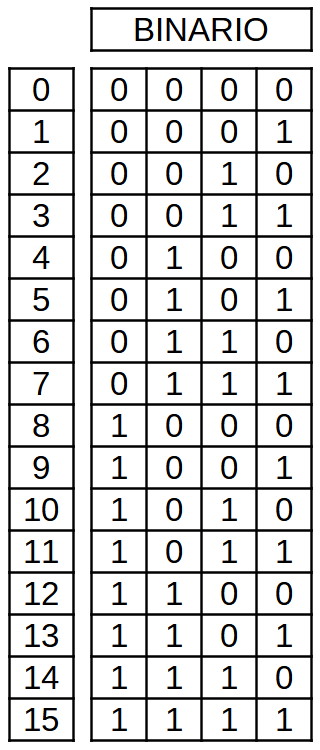
The following table shows the first 16 numbers in decimal and binary, starting with zero and ending with the value fifteen:

As you can see, there are certain rules in binary numbers that can help us build the table with the binary count:

1. In binary they only use the digits zero and one.
2. Decimal zero corresponds to all binary digits to zero.
3. The rightmost binary digit, which is the one with the least value, constantly changes from zero to one as we count one more number. 0 1 0 1 0 1 0 1 ...
4. The second binary digit starting from the right changes every two numbers from zero to one. 0 0 1 1 0 0 1 1 ...
5. The third binary digit starting from the right changes every four numbers from zero to one. 0 0 0 0 1 1 1 1 ...
6. The fourth binary digit starting from the right, which is the one with the highest value, changes every eight numbers from zero to one. 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1.

Decimal to Binary Conversion

Humans are used to counting and seeing numbers in decimal notation, so it is convenient to know how to convert any decimal number to binary notation.

To convert a decimal number to binary we will divide the number by two consecutively until there is no value left to divide. The binary number will come from the remainders of the consecutive divisions, so that the first remainder obtained will be the binary digit with the least weight and the last remainder obtained will be the binary digit with the greatest weight:

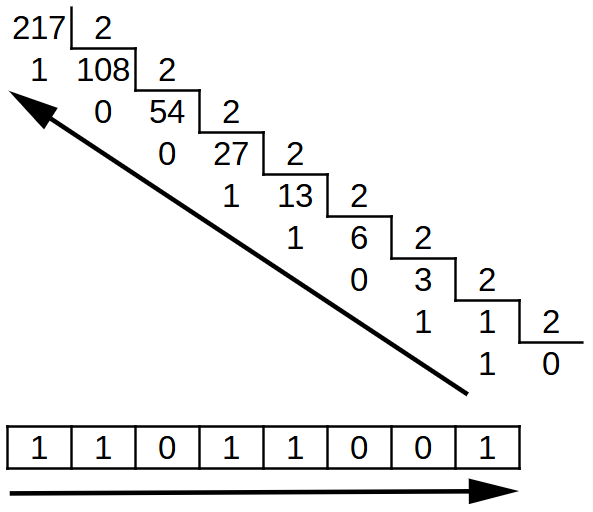
Process to convert a decimal number to binary by dividing consecutively by two.

Another example of converting the decimal number 146 to binary:

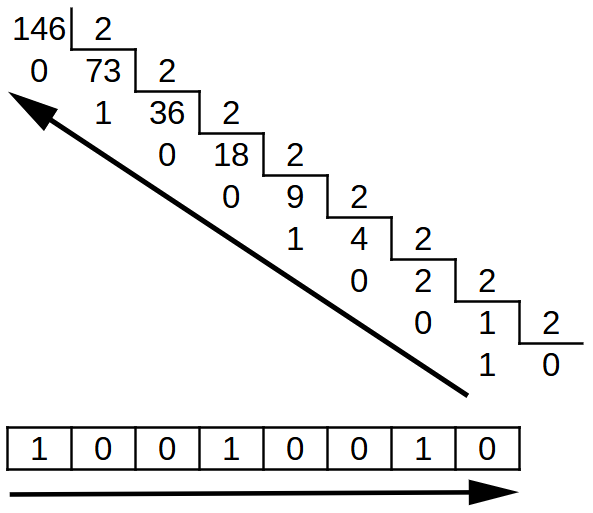
Process to convert a decimal number to binary by dividing consecutively by two.

Binary to decimal conversion

A simple way to convert a binary number to a decimal number is to create a table with the value of each binary digit.

The first binary digit to the right, the one with the smallest value, has a value of one (1). The second binary digit from the right has a value of two (2). The values ​​increase like this, multiplying by two. In the eighth position, the value of the binary digit is 128.

Once the table of the values ​​of each binary digit has been constructed, it is only necessary to add those values ​​that correspond to a one in the binary number:

Binary to decimal conversion.

Exercises

1. Make a table with the binary numbers from zero to 31 using the rules described in the 'Counting in binary' section.

2. Convert the following numbers from decimal to binary:

   97

   137

   156

   229

   245

3. Convert the following numbers from binary to decimal:

   1 0 0 0 1 1 1 1

   1 0 1 0 0 1 1 0

   1 1 0 0 0 1 1 1

   1 1 1 0 1 1 0 0

   1 1 1 1 1 1 0 1