8. THE LOGIC gate XOR

The Xor logic gate has two or more entries and one way out.

The output has a high logical value (1) If the sum of the inputs is an odd value.

That is, if the entrance to or input B are at high level, but not both at the same time, the output will be at high level. Hence the name of eXclusive OR in English.

The gate symbol XOR is as follows:

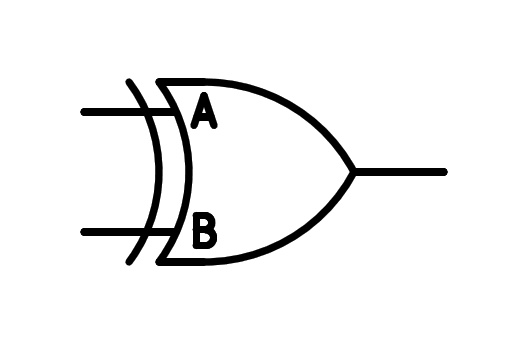
Puerta lógica XOR de dos entradas.

Two -entry logic gate symbol.

The logical function of the xor gate is represented by a sum symbol surrounded by a circle, so that the exit of the gate will be the exclusive logic of the entries:

Out = A \oplus B

The Truth Table XOR is as follows:

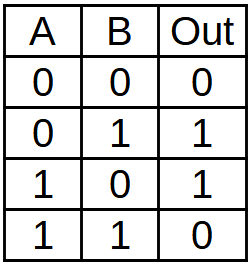
Tabla de verdad de la puerta lógica XOR de dos entradas.

Truth Table of the Logic gate Xor of two entries.

If the two entrances are worth zero, the exit will be worth zero, if any entry is worth one, the exit will be worth one and if the two entrances are worth one, the exit will be valued again.

Xor gate applications

  1. The Xor gate can be used to calculate the parity value of all its inputs, so that the entries next to the output will always have an even value of some.
  2. Another xor gate application is to make arithmetic bits sums. The Xor gate calculates the arithmetic sum of two bits and the gate and calculates the hauling of adding two bits.
  3. Another Xor gate application is to invest or not invest the value of entry B depending on the entrance to:
    • If the entrance to outer zero, input B is copied the same at the output.
    • If the entrance to Vale one, the entrance B is copied inverted in the exit.

Simulation

In the following simulation we can see the operation of the Xor logic gate.

Exercises

  1. Explain with your words the functioning of the logic gate Xor.

  2. Draw the symbol of the XOR logic gate of two entries, its logical function and its truth table.

  3. Briefly explain three applications of the logic gate Xor.

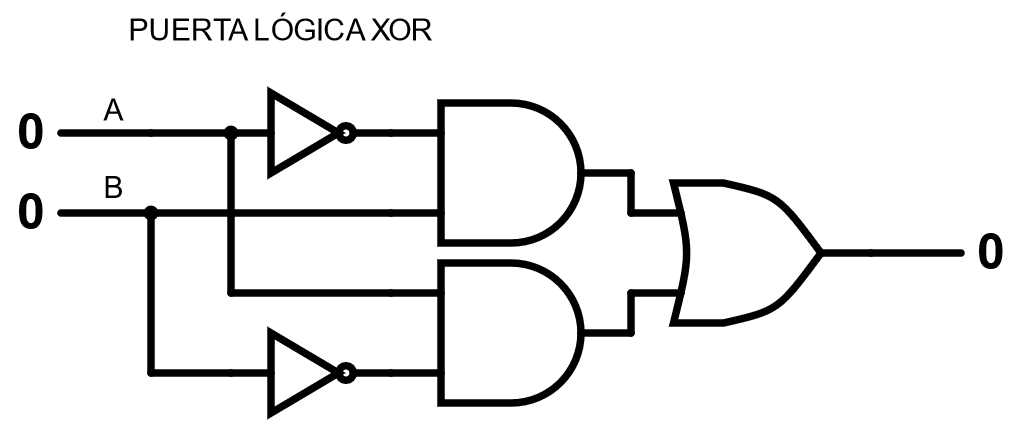
  4. In the simulator, copy the circuit that appears in the following image to emulate the operation of the gate Xor through Not, OR and AND:

    Puerta XOR simulada con puertas NOT, OR y AND.

    Check that its operation is equal to the gate Xor.

  5. Draw a logical gate of three entries, its logical function and its truth table.

    To perform the gate's truth table, remember that the exit is worth one if the entrance bits are odd.